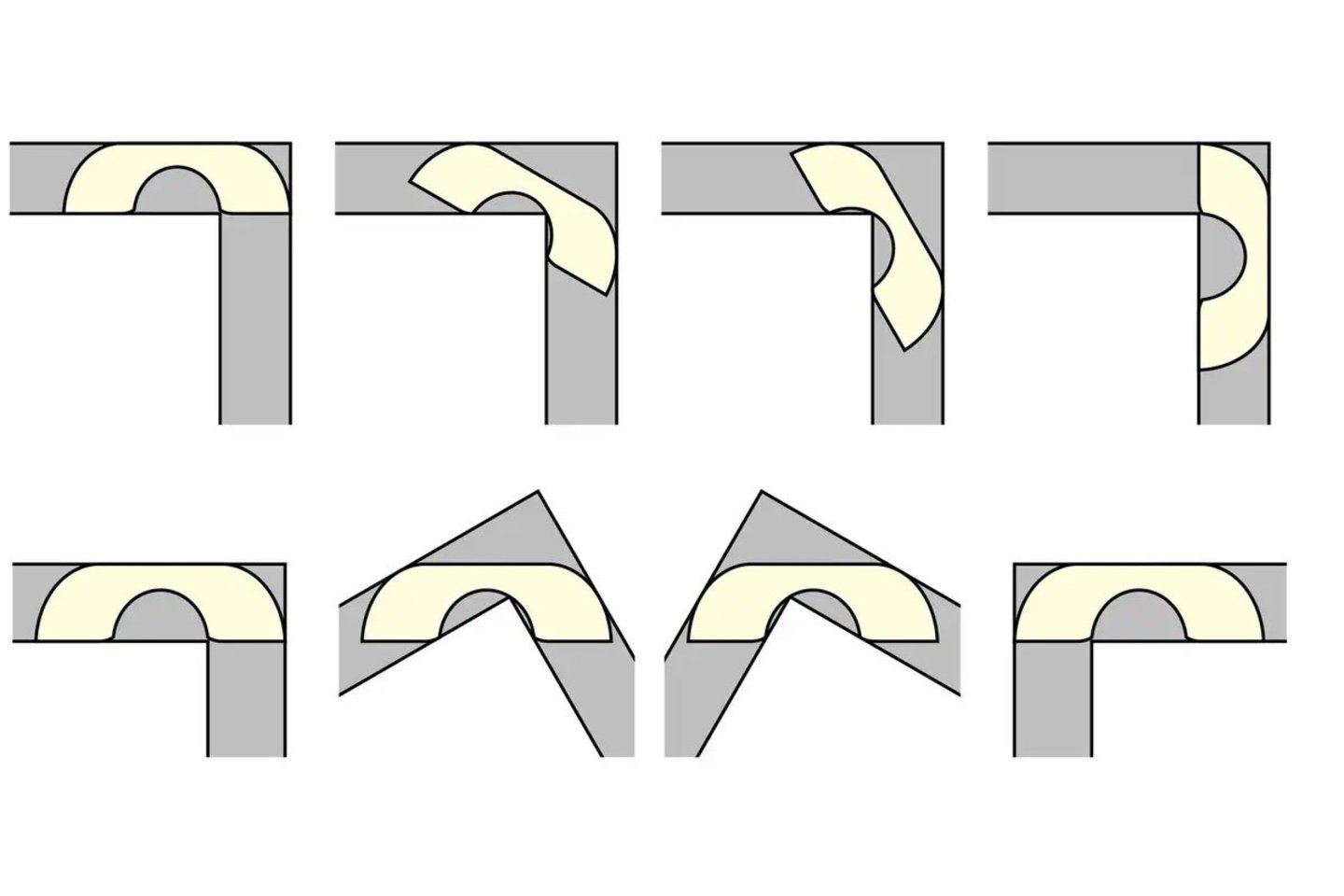
Sunkumai, susiję su didelių baldų įnešimu į namus, pažįstami daugeliui žmonių – tačiau matematikai ypač susidomėjo perkeliamos sofos problema nuo tada, kai 1966 m. ją pirmą kartą iškėlė Leo Moseris. Uždavinyje daroma prielaida, kad bandoma pernešti dvimatę sofą (taigi nekreipiant dėmesio į jos aukštį) per koridorių su 90 laipsnių posūkiu – ir klausiama, ar įmanoma apskaičiuoti didžiausią ploto formą, su kuria tai įmanoma.
Matematikai netrukus nustatė, kad seną telefono ragelį primenanti forma, regis, leidžia sukurti didžiausius plotus, o 1992 m. Josephas Gerveris iš Rutgerso universiteto JAV atrado konkrečią tokią formą, sudarytą iš 18 lenktų dalių, kuri ir užėmė pirmąją vietą. Vėlesniais metais mokslininkai sunkiai rado didesnių sofų ir ėmė įtarti, kad „Gerverio sofa“ gali būti didžiausias įmanomas sprendimas – tačiau niekas negalėjo įrodyti, kad, taip sakant, už kampo nesislepia dar didesnė sofa.
Dabar Jineonas Baekas iš Pietų Korėjos Yonsei universiteto daugiau nei 100 puslapių apimančiame tyrime įrodė, kad Gerverio sprendimas iš tiesų yra didžiausias įmanomas, ir oficialiai išsprendė 58 metų senumo problemą. J. Baekas, pradėjęs spręsti šį galvosūkį prieš septynerius metus, teigia, kad įrodymo kontūrus jis sugalvojo maždaug po dvejų metų darbo su problema, tačiau prireikė dar penkerių metų, kad būtų išsiaiškintos visos detalės.
J. Baeko įrodymas pirmiausia sutelkia dėmesį į nedidelį galimų sofų pasirinkimą ir, naudodamasis tuo, įrodo tam tikras savybes, kuriomis turi pasižymėti didžiausia sofa. Tarp jų yra santykinai lygi išorė, parametras, vadinamas balansu, kuris yra susijęs su simetrija, ir, žinoma, lemiamas gebėjimas pasukti už kampo visu 90 laipsnių kampu.
Remdamasis šiomis savybėmis, J. Baekas sugalvojo naują matematinį dydį, glaudžiai susijusį su plotu, pavadintą Q, kuris palengvino problemos analizę. Tai reiškė, kad iš atviro scenarijaus, vadinamo nekonveksine problema, buvo galima paversti problema su apibrėžtais – arba išgaubtais – sprendiniais: pavyzdžiui, rutuliukas rieda į dubens dugną, o ne į abi kalvos puses. Tada J. Baekas nustatė, kad didžiausia Q reikšmė yra tikslus Gerverio pasiūlytas sprendinys, taip įrodydamas, kad jokia kita sofa negali būti didesnė.
„Žinoma, esu labai laimingas dėl viso to, – sako J. Gerveris. „Man 75-eri, o J. Baekui ne daugiau kaip 30 metų. Jis turi daug daugiau energijos, ištvermės ir išlikusių smegenų ląstelių nei aš, todėl džiaugiuosi, kad jis perėmė estafetę. Taip pat labai džiaugiuosi, kad gyvenau pakankamai ilgai, kad galėčiau pamatyti, kaip jis užbaigia tai, ką aš pradėjau“.
Įrodymą dar turi iki galo patikrinti kiti matematikai, todėl yra tikimybė, kad jame yra klaidų, tačiau J. Baekas tikisi, kad jis teisus. „Negaliu sakyti, kad esu įsitikinęs 100 procentų, nes esame žmonės, darome klaidų, bet vis dėlto padariau viską, kad būčiau kuo labiau įsitikinęs“, – sako jis.
Tyrimas paskelbtas „arXiv“.
Parengta pagal „New Scientist“.