Ar egzistuoja figūra, tobulesnė už apskritimą? Tikrai taip Mokslo populiarinimo konkursas

Pradėkime nuo to, kad kaip apskritimo tūrinis formatas vadinamas rutuliu, taip ir elipsinis trimatis kūnas yra vadinamas elipsoidu. Ir ne, tai nėra kiaušinis – tačiau panašus į jį, tik neturi smailiosios pusės ir todėl Velykų metu netinkamas naudoti žaidimams prie stalo.

Elipsoidas gamtoje sutinkamas labai dažnai. Įvairūs dangaus kūnai – tame tarpe ir mūsų Žemė – yra elipsoido formos, mat dėl savo sukimosi apie ašį šiek tiek susiploja. Saulė taip pat yra elipsoidas, mūsų galaktika – elipsės formos, o orbita, kuria skriejame apie Saulę irgi yra elipsinė.

Tiesą sakant, gamtoje tobulų apskritimų apskritai nesutiksime, o ką pastebėsime, tai būtent elipsės formos objektus.

Pirmą kartą elipses studijavo graikų matematikas, Aleksandro Didžiojo matematikos mokytojas Menaekmusas (Menaechmus), gyvenęs IV amžiuje prieš mūsų erą. Nieko keisto, kad pavadinimą šiai figūrai davė Apolonijus savo darbe „Kūgiai“ – mat šis graikų matematikas buvo laikomas „Didžiuoju geometriku“. Kiek vėliau, praėjus vos 900 metų, Kepleris padarė atradimą, kad Marso orbita yra elipsės formos.

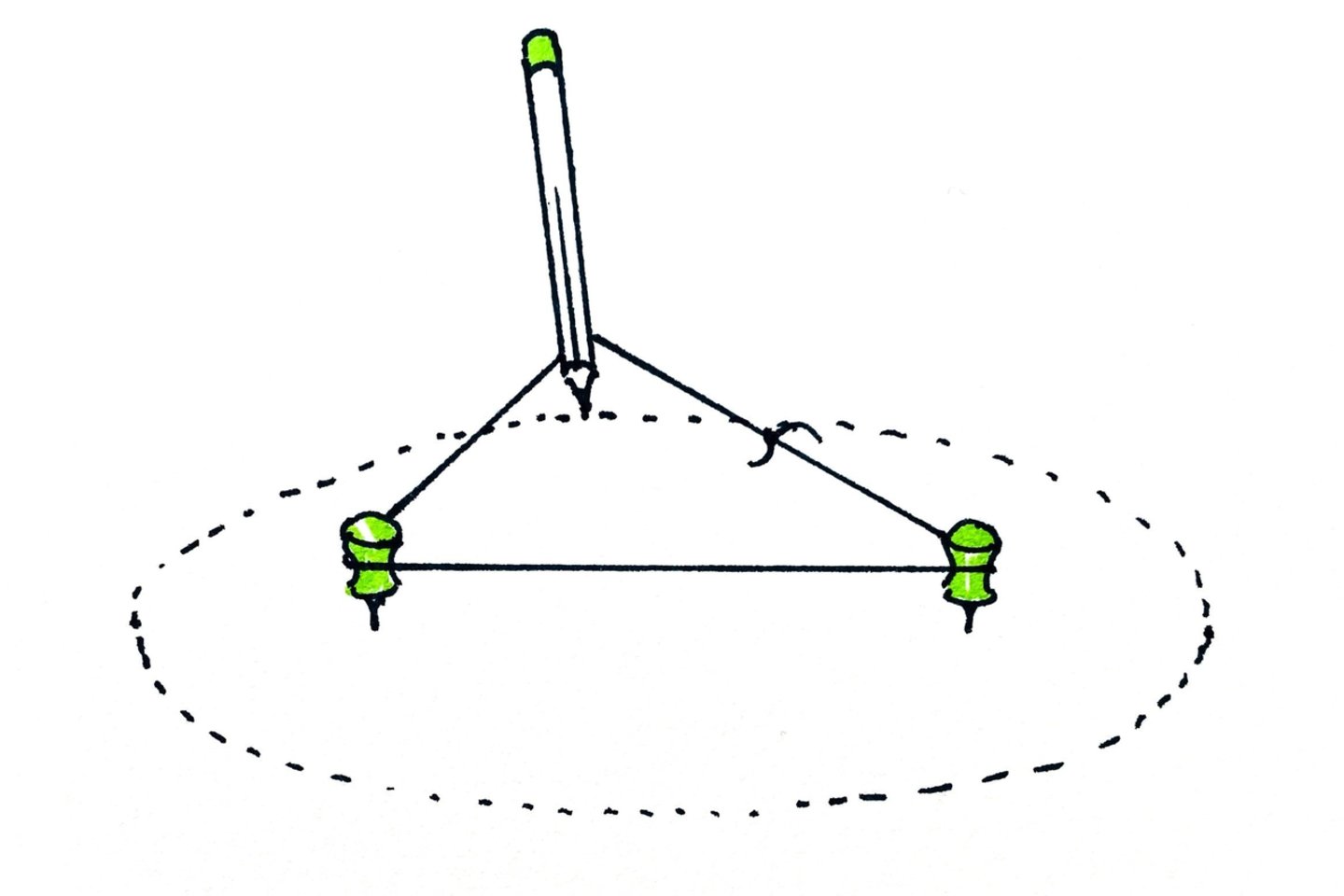
Norint suvokti elipsės savybes ir jomis tinkamai pasidžiaugti, labai pravartu žinoti, kaip ją „pasigaminti“ – t. y. nusibrėžti ant popieriaus. Visų pirma, pasiimkite popieriaus lapą ir pasižymėję jame du taškus, įsmeikite į juos du smeigtukus. Dabar pasiimkite surištą siūlą ir pieštuką. Apvykite siūlu smeigtukus ir įstatę pieštuką į siūlą įtempdami brėžkite kreivę. Gautas rezultatas – taisyklinga elipsė. Taškai, kur įbedėte du smeigtukus, yra vadinami elipsės židiniais.

Iš šio brėžimo būdo nesunkiai suvoksime vieną pagrindinių elipsės savybių – atstumų, einančių iš elipsės židinių iki bet kurio elipsės krašto taško, suma yra visada vienoda. Jeigu tą patį atliksime su vienu smeigtuku, gausime apskritimą. Taigi, apskritimas yra vienas iš elipsės tipų, kurio abu židiniai yra viename taške.

Yra ir kitų būdų, kaip gauti elipsę. Pavyzdžiui, žiūrint į apskritimą iš perspektyvos, gausime elipsę. Kreivai nupjovus kūgio formos smėlio pilį paplūdimyje, taip pat gausime elipsės formos paviršių.

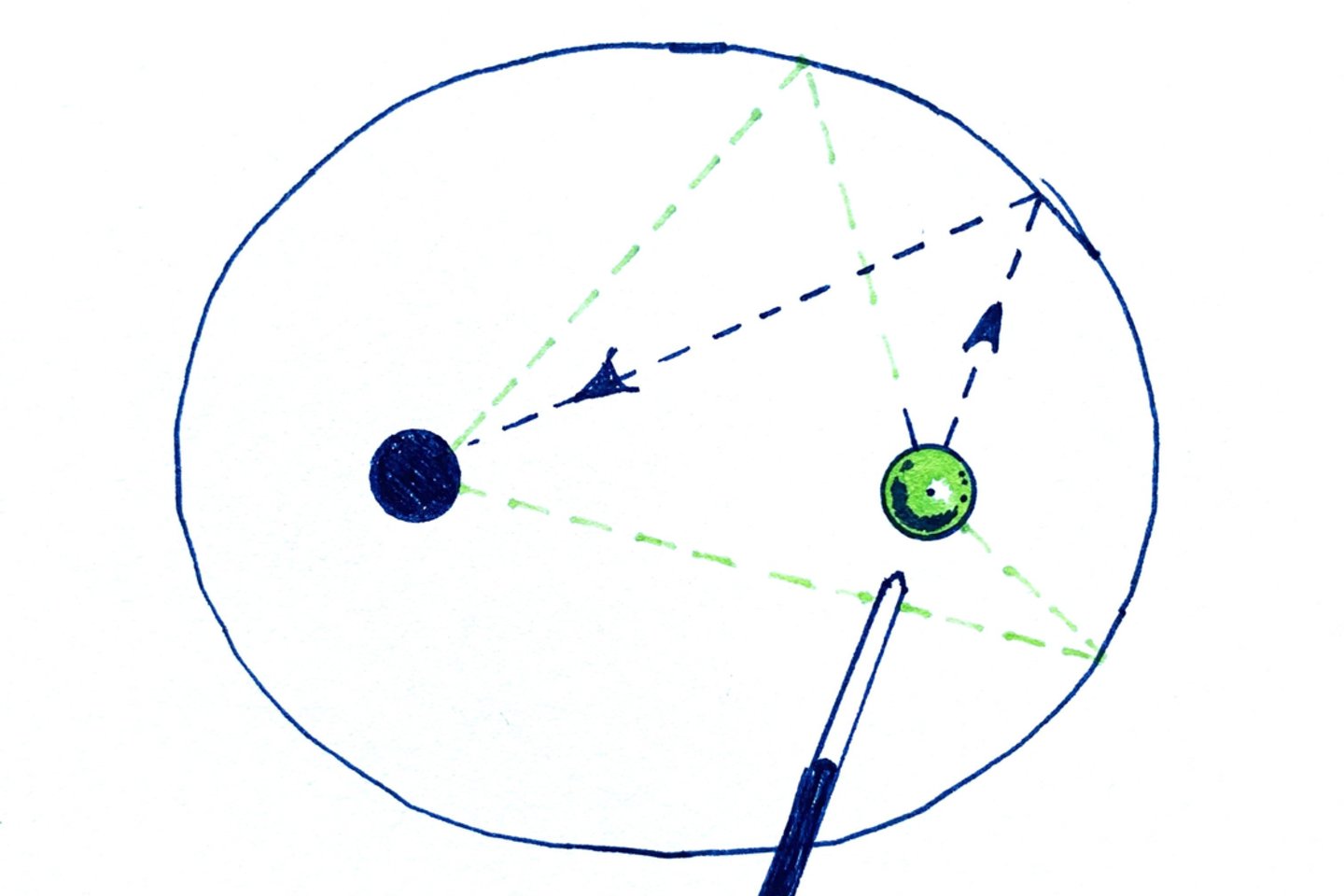
Ir čia įdomumai tik prasideda. Žinodami elipsės savybes, galime sugalvoti įspūdingų ir beprotiškų idėjų jų pritaikymui mūsų kasdieniame gyvenime. Vienas tokių pritaikymų yra elipsės formos biliardo stalas, kuriame pažymėti abu elipsės židiniai. Viename iš židinių yra išpjauta skylė biliardo rutuliui įkristi. Jeigu mušame rutulį iš vieno židinio į bet kurią stalo sienelės vietą tiesia linija, tai rutulys neišvengiamai atsidurs kitame židinio taške – taigi, įkris į skylę. Žinoma, nereikėtų persistengti ir mušti derėtų ne per stipriai, kad rutulys nepralėktų pro šalį.

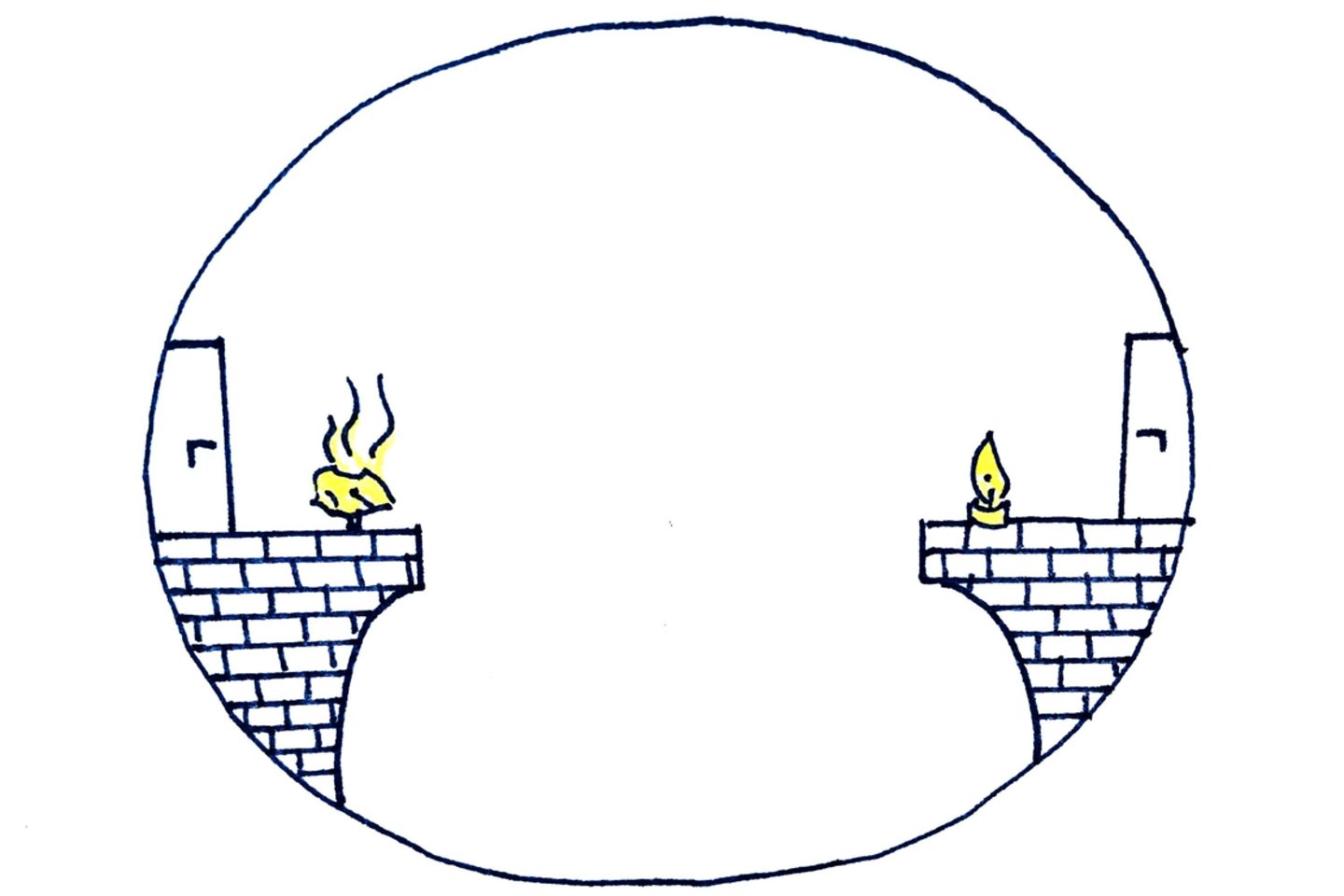
Įsivaizduokite elipsoido formos patalpą, kurioje sienos išklotos veidrodžiais – ir pažymėti abu židinio taškai. Padėję viename jų popieriaus skiautelę, o kitame – uždegę žvakę, pamatysime, kad popierius pradės degti. Panašiu principu veikia ir taip vadinami kuždesių kambariai. Jeigu viename elipsoido židinio taške kažką sušnabždėsite, o kitame taške bus klausytojas, tai net jei patalpoje vyraus triukšmas, klausytojas išgirs jūsų slaptą žinutę.

Elipsoido savybės taikomos ne tik akustikoje, bet ir optikoje – pavyzdžiui, teleskopų lęšių ar lazerių sistemų gamyboje.

Taigi, atsižvelgus į paminėtas elipsės savybes, galbūt apskritimas jau nebeatrodys toks išskirtinis ir unikalus – o elipsė pasirodys esanti verta daugiau dėmesio, negu anksčiau.